SET Theory

                                              Set Theory

                          Set : A set is a well-defined collection of objects.

           Types of set:

            ⇒ Roaster or Tabular form                                 

              ⇒Set builder form

1. The Empty set : It is also called void set or null set.It is denoted by {} or Φ.

1. Finite and Infinite set : A set which consists of a finite number of element is called finite set . Otherwise the set is called an infinite set.

1. Subset : A set A is said to be a subset of set B.It is denoted by A⊂B if a ∈ A ⇒a ∈ B.

 We denoted :         Set of real numbers by R        Set of  natural numbers by N        Set of integer by Z       Set of rational numbers by Q      Set of irrational numbers by T

   

                               

Power Set

A Power Set is a set of all the subsets of a set. It is denoted by P(S).

the Power Set of {a,b,c}:

P(S) = { {}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} }

The Universal Set

In previous lessons, we learned that a set is a group of objects, and that Venn diagrams can be used to illustrate both set relationships and logical relationships.

Example 1: Given A = {1, 2, 5, 6} and B = {3, 9}, what is the relationship between these sets?

A and B have no elements in common. This relationship is shown in the Venn diagram below.

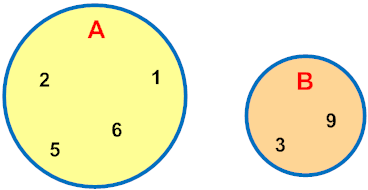
Answer: A and B have no elements in common. These sets do not overlap.

VENN Diagrams

A Venn diagram in which the area of each shape is proportional to the number of elements it contains is called an area-proportional or scaled Venn diagram.

Set Operations : The four basic operations are:

1. Union of Sets

2. Intersection of sets

3. Complement of the Set

4. Cartesian Product of sets

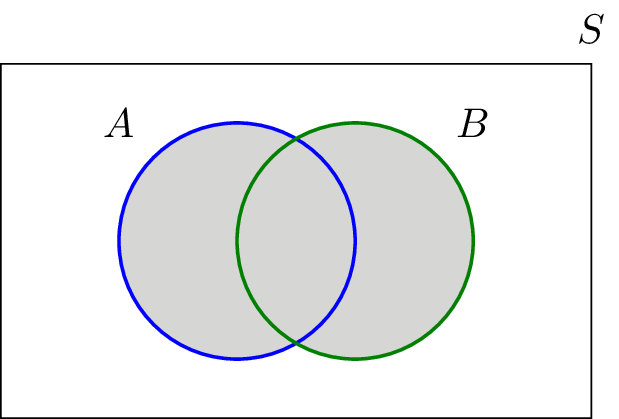
The union of two sets is a set containing all elements that are in 

A$A$ or in B$B$ (possibly both). For example, {1,2}∪{2,3}={1,2,3}$\{1,2\}\cup \{2,3\}=\{1,2,3\}$. Thus, we can write x∈(A∪B)$x\in (A\cup B)$ if and only if (x∈A)$(x\in A)$ or (x∈B)$(x\in B)$. Note that A∪B=B∪A$A\cup B=B\cup A$. In Figure 1.4, the union of sets A$A$ and B$B$ is shown by the shaded area in the Venn diagram.

The shaded area shows the set B∪A$B\cup A$.

Definition of Intersection of Sets:

Intersection of two given sets is the largest set which contains all the elements that are common to both the sets.

To find the intersection of two given sets A and B is a set which consists of all the elements which are common to both A and B.

The symbol for denoting intersection of sets is ‘∩‘.

For example:

Let set A = {2, 3, 4, 5, 6}

and set B = {3, 5, 7, 9}

In this two sets, the elements 3 and 5 are common. The set containing these common elements i.e., {3, 5} is the intersection of set A and B.

The symbol used for the intersection of two sets is ‘∩‘.

Therefore, symbolically, we write intersection of the two sets A and B is A ∩ B which means A intersection B. 

The intersection of two sets A and B is represented as A ∩ B = {x : x ∈ A and x ∈ B} 

Solved examples to find intersection of two given sets:

1. If A = {2, 4, 6, 8, 10} and B = {1, 3, 8, 4, 6}. Find intersection of two set A and B. 

Solution:

A ∩ B = {4, 6, 8}

Therefore, 4, 6 and 8 are the common elements in both the sets. 

Some properties of the operation of intersection

(i) A∩B = B∩A (Commutative law)

(ii) (A∩B)∩C = A∩ (B∩C) (Associative law)

(iii) ϕ ∩ A = ϕ (Law of ϕ)

(iv) U∩A = A (Law of ∪)

(v) A∩A = A (Idempotent law) 

(vi) A∩(B∪C) = (A∩B) ∪ (A∩C) (Distributive law) Here ∩ distributes over ∪

Also, A∪(B∩C) = (AUB) ∩ (AUC) (Distributive law) Here ∪ distributes over ∩

Notes:

A ∩ ϕ = ϕ ∩ A = ϕ i.e. intersection of any set with the empty set is always the empty set.