NIMCET Preparation Tips

100 % NIMCET Exam  crack  करना मैं  गारंटी  लेटी  हूँ !

NIT entrance exam book

 $3.95 = 308.94 Rupees

50% off on this book. This book is very good   and inside the book their  are many tips and tricks are available

https://amzn.to/2MEDBal

Computer Awareness book for NIMCET

अब  NIMCET  Exam  Crack  करना  हुआ आसान !
आप इस  computer  awareness  book  को  खरीदिए               
इस  book  पे  click  kijiye  यहां  👇👇👇👇👇

50% off के  साथ  😀😀😀

                                                      

NIMCET Previous Year question practice

Download this link👇👇👇👇👇

https://drive.google.com/file/d/1gzqHesqcEckEZh0Yf17UR2THQJAOAGMz/view?usp=sharing

Set Theory objective Questions......

Download this link.....👇👇👇👇👇👇👇

https://drive.google.com/file/d/1Dd-dYPfPSXKYWAMaxbL-x-VjrPgBleIG/view?usp=sharing

अब NIMCET Entrance Exam Crack करना हुआ आसान

अब  NIMCET Entrance Exam Crack करना  हुआ  आसान but उसके  लिए  आपलोगों  को follow करना होगा इस Rule को..... 

1. आप  follow कीजिए  इस  website-pammy809.blogspot.com को। 

1. watching uploading videos and notes......

मैं  गारंटी  लेती  हूँ  आपसब  इस  exam  को   जरूर crack  किजिएगा।...

NIT MCA Common Entrance Test is the national level entrance test in India for admission to Master of Computer Applications courses in selected National Institutes of Technology, University of Hyderabad, Guru Gobind Singh Indraprastha University and in Harcourt Butler Technical University. 

 

SET Theory

                                              Set Theory

                          Set : A set is a well-defined collection of objects.

           Types of set:

            ⇒ Roaster or Tabular form                                 

              ⇒Set builder form

1. The Empty set : It is also called void set or null set.It is denoted by {} or Φ.

1. Finite and Infinite set : A set which consists of a finite number of element is called finite set . Otherwise the set is called an infinite set.

1. Subset : A set A is said to be a subset of set B.It is denoted by A⊂B if a ∈ A ⇒a ∈ B.

 We denoted :         Set of real numbers by R        Set of  natural numbers by N        Set of integer by Z       Set of rational numbers by Q      Set of irrational numbers by T

   

                               

Power Set

A Power Set is a set of all the subsets of a set. It is denoted by P(S).

the Power Set of {a,b,c}:

P(S) = { {}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} }

The Universal Set

In previous lessons, we learned that a set is a group of objects, and that Venn diagrams can be used to illustrate both set relationships and logical relationships.

Example 1: Given A = {1, 2, 5, 6} and B = {3, 9}, what is the relationship between these sets?

A and B have no elements in common. This relationship is shown in the Venn diagram below.

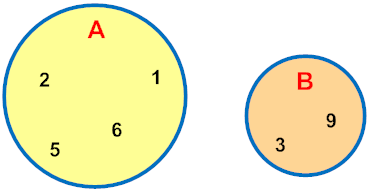
Answer: A and B have no elements in common. These sets do not overlap.

VENN Diagrams

A Venn diagram in which the area of each shape is proportional to the number of elements it contains is called an area-proportional or scaled Venn diagram.

Set Operations : The four basic operations are:

1. Union of Sets

2. Intersection of sets

3. Complement of the Set

4. Cartesian Product of sets

The union of two sets is a set containing all elements that are in 

A$A$ or in B$B$ (possibly both). For example, {1,2}∪{2,3}={1,2,3}$\{1,2\}\cup \{2,3\}=\{1,2,3\}$. Thus, we can write x∈(A∪B)$x\in (A\cup B)$ if and only if (x∈A)$(x\in A)$ or (x∈B)$(x\in B)$. Note that A∪B=B∪A$A\cup B=B\cup A$. In Figure 1.4, the union of sets A$A$ and B$B$ is shown by the shaded area in the Venn diagram.

The shaded area shows the set B∪A$B\cup A$.

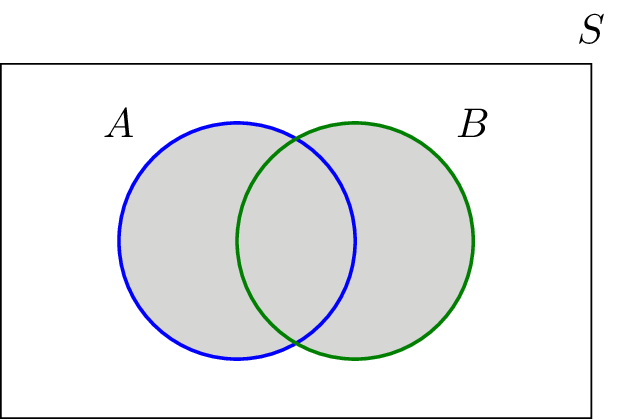
Definition of Intersection of Sets:

Intersection of two given sets is the largest set which contains all the elements that are common to both the sets.

To find the intersection of two given sets A and B is a set which consists of all the elements which are common to both A and B.

The symbol for denoting intersection of sets is ‘∩‘.

For example:

Let set A = {2, 3, 4, 5, 6}

and set B = {3, 5, 7, 9}

In this two sets, the elements 3 and 5 are common. The set containing these common elements i.e., {3, 5} is the intersection of set A and B.

The symbol used for the intersection of two sets is ‘∩‘.

Therefore, symbolically, we write intersection of the two sets A and B is A ∩ B which means A intersection B. 

The intersection of two sets A and B is represented as A ∩ B = {x : x ∈ A and x ∈ B} 

Solved examples to find intersection of two given sets:

1. If A = {2, 4, 6, 8, 10} and B = {1, 3, 8, 4, 6}. Find intersection of two set A and B. 

Solution:

A ∩ B = {4, 6, 8}

Therefore, 4, 6 and 8 are the common elements in both the sets. 

Some properties of the operation of intersection

(i) A∩B = B∩A (Commutative law)

(ii) (A∩B)∩C = A∩ (B∩C) (Associative law)

(iii) ϕ ∩ A = ϕ (Law of ϕ)

(iv) U∩A = A (Law of ∪)

(v) A∩A = A (Idempotent law) 

(vi) A∩(B∪C) = (A∩B) ∪ (A∩C) (Distributive law) Here ∩ distributes over ∪

Also, A∪(B∩C) = (AUB) ∩ (AUC) (Distributive law) Here ∪ distributes over ∩

Notes:

A ∩ ϕ = ϕ ∩ A = ϕ i.e. intersection of any set with the empty set is always the empty set.

BASIC COMPUTER

                                              COMPUTER

Computer: A Computer is a General purpose machine, commonly consisting of digital circuitry, that accepts (inputs), stores, manipulates, and generates (outputs) data as numbers, text, graphics, voice, video files, or electrical signals, in accordance with instructions called a program.

• Father of the computer – Charles Babbage.
• Father of the modern computer – Alan Turing.
• Basic Architecture of Computer: John Von Neumann (1947-49).
• First Programmer: Lady Ada Lovelace (1880).
• First Electronic Computer: ENIAC (1946) – J.P. Eckert & J.W. Mauchly.
• The first computer for the home user introduced – IBM in 1981.

Full form of Computer:

• C – Commonly
• O – Operated
• M – Machine
• P – Particularly
• U – Used for
• T – Technical
• E-Education
• R – Research
Characteristics of Computer
• Speed
• Accuracy
• Storage
• Diligence
• Versatility
• Automation
Computer – An Introduction
• A computer is a device that can receive process and store data.
• However, all computers have several parts in common:
• Input devices allow data and commands to the computer (Mouse, Keyboard etc.)
• Memory for storing commands and data.
• Central Processing Unit which controls the processing.
• Monitor Process the information in the form of output.

Types of computers

Computers range in size and capability. There are supercomputers, very large computers with thousands of microprocessors that perform extremely complex calculations.
There are tiny computers embedded in cars, TVs, stereo systems, calculators, and appliances. These computers are built to perform a few number of tasks.
Desktop computers
1. Desktop computers design is made for use at a desk or table.
2. They are typically larger and more powerful than other types of personal computers.

Peripheral Devices

1. The peripheral device connects to a computer system to add functionality. Examples are a mouse, keyboard, monitor, printer and scanner.
2. A computer peripheral is a device that connects to a computer but is not part of the core computer architecture.
3. The core elements of a computer are the central processing unit, power supply, motherboard and the computer case that contains those three components.

Types of Peripheral Devices

• There are many peripheral devices, but they fall into three general categories:
• Input devices, such as a mouse and a keyboard
• Output devices, such as a monitor and a printer
• Storage devices, such as a hard drive or flash drive

Computer Knowledge – Main Parts of Computer

Hardware
• Computer hardware is what you can physically touch includes the computer case, monitor, keyboard, and mouse.
• It also includes all the parts inside the computer case, such as the hard disk drive, mo
• there-board, video card, and many others.
Input Devices
• In computing, an input device is a peripheral (piece of computer hardware equipment) used to 
• e data and control signals to an information processing system.
• It will control devices such as a computer or information appliance.
Examples: keyboards, mice, scanners, digital cameras and joysticks.

complement's.....

  ⇒ 1's complement

 ⇒ 2's complement

  

Binary addition......

part-4 universal gate

part-3 Logic gates..

आज  हमलोग  सीखेंगे  Logic gate...  

previous year question for practice......

Practice this question for NIMCET........👇👇👇👇

Number System part-2....

आज  हम  सीखेंगे किसी  भी  Digit  को binary, decimal, octal, and hexadecimal number system में  कैसे  बदलना (convert) करना  हैं !!

part - 1 Trick of covert digit into binary number...

Part-1 Computer basic..👇👇👇👇

Notes of Probability and Statistics....

आज  हम  सीखेंगे  Probability and Statistics........

Download PDF..👇👇

https://drive.google.com/file/d/view?usp=sharing

Important Notes for NIMCET

Basic computer

Some mathematical formulas

Probability

    Probability

Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur or how likely it is that a proposition is true. Probability is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility and 1 indicates certainty. 

example : It will probably rain today.

              :It doubt that he will pass  the test.

           Types of  probability : 

1. An Experimental approach

2. Axomatic approach

Introduction :-

• Event

• Sample Space

• Exhaustive cases

Event :- Let E be the event of any Experiment, and their outcome be probably defined, then total no. of Event is denoted by n(E).

Sample Space :- It is collection of all event.It is denoted by 's'.

                          let E1,E2,------------,En be the event.             then             S={E1,E2,E3,-------------,En}            n(s) = n.Probability Event :- Let E be the event and s be the sample space then the probability is defined as p(E)
                     total number of events   p(E)   =  ---------------------------------                     total  number of outcome         i.e   p(E) = n(E) / n(S)where 0<=p(E)<=1
Q. When one coin is tossed what is probability of getting tail .     let E be the event           S =  {H,T}  n(S) = 2
           E = {T}  n(E) = 1
       p(E) = n(E) / n(S)   1 / 2

Q.    what is probability of getting head.

             let E be the event  

           S =  {H,T}  n(S) = 2
           E = {H}  n(E) = 1
       p(E) = n(E) / n(S)   1 / 2

Dependent and independent events

Independent events

Two events, A and B are independent if and only if

     P(A and B)=P(A)×P(B)

Independence

Roll a single 6$\text{6}$-sided die and consider the following two events:

• E: you get an even number
• T: you get a number that is divisible by three

Now answer the following questions:

• What is the probability of E?
• What is the probability of getting an even number if you are told that the number was also divisible by three?
• Does knowing that the number was divisible by 3 change the probability that the number was even?

Are the events E and T dependent or independent according to the definition? (Hint: compute the probabilities in the definition of independence.)

The probability of A is the ratio between the number of outcomes in A and the number of outcomes in the sample space, S.

P(A)=n(A)n(S)

Now, let's say that we know that event B happened. How does this affect the probability of A? Here is how the Venn diagram changes:

A lot of the possible outcomes (all of the outcomes outside B) are now out of the picture, because we know that they did not happen. Now the probability of A happening, given that we know that B happened, is the ratio between the size of the region where A  is present (A and B) and the size of all possible events (B).

P(A if we know B)=n(A and B)n(B)